Before you understand Remainder Theorem, you are advised to read:
What is Dividend, Divisor, Quotient & Remainder ?
What is Degree of a Polynomial ?
How to Find Value Polynomial ?
How to divide Polynomial by Binomial ?
(This Remainder Theorem applies to situation where a polynomial is divided by a linear polynomial)
Remainder Theorem says that, " If p(x) is divided by linear polynomial (x - a), then remainder will always be p(a) ".
Here, p(x) can be any polynomial of degree greater than or equal to zero. And 'a' can be any real number.
Lets prove this Theorem with the help of following examples:
Example 1: Divide (x3 + 4) by (x - 1)
Solution: As per the given question:
Polynomial = Dividend= (x3 + 4)
Linear Polynomial = Divisor = (x - 1)
Division is done as shown below:
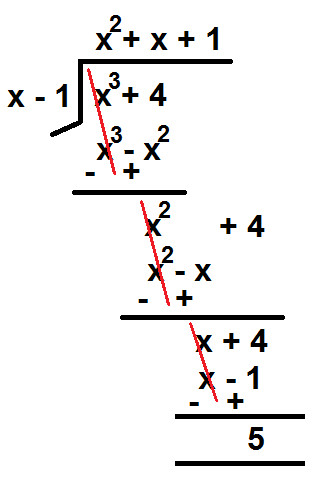
Hence, when (x3 + 4) is divided by (x - 1), we get:
Quotient = (x2 + x + 1)
Remainder = 5.... (Statement 1)
Now, let's apply remainder theorem on the same example:
Remainder Theorem says that, " If p(x) is divided by linear polynomial (x - a), then remainder will always be p(a) ".
Apply the values from given example and we get:
Polynomial p(x) = (x3 + 4)
Linear Polynomial (x - a) = (x - 1)
So value of a = 1
And as per remainder theorem, x = a = 1
Now find the value of p(x) = (x3 + 4), where x = 1 and we get:
p(1) = (1)3 + 4
= 1 + 4 = 5 .... (Statement 2)
Hence, as per statement 1 and 2, Remainder is same i.e. 5.
This proves the remainder theorem.
|






