| △ ABC is right angle triangle at B, AB=8, BC=11, AC=13. Write sin C, cos A, tan C |
Lets draw the right angle triangle with the above mentioned details
Given thing are
Right angle at B
Theta Angle at C (As mentioned in statement sin C, tan C that means angle C should be taken as Theta)
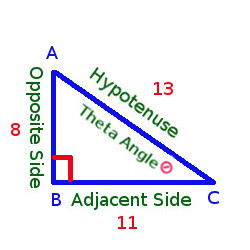
Hypotenuse : AC = 13
Opposite Side : AB = 8 (Opposite to ∠ Θ)
Adjacent Side : BC = 11 (Adjacent to ∠ Θ)
Sin C = Opposite Side/Hypotenuse = 8/13
Tan C = Opposite Side/Adjacent = 8/11
For Cos the Theta Angle is at A (As mentioned in statement "Cos A" that means angle A should be taken as Theta)
As cos angle is now A, the adjacent side and opposite side of the triangle will be as below
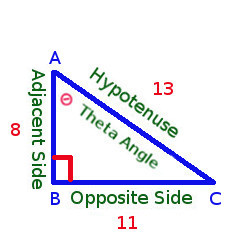
You will see that Theta angle is now at A, So
Hypotenuse : AC = 13
Opposite Side : BC = 11 (Opposite to ∠ Θ)
Adjacent Side : AB = 8 (Adjacent to ∠ Θ)
So, cos A = Adjacent Side/Hypotenuse = 8/13
|
Related Question Examples
|
△ ABC is right angle triangle at B, AB=8, BC=11, AC=13. Write sin C, cos A, tan C |
|
△ PQR is right angle triangle at P, PQ=9, QR=11, RP=7. Write sin Q, cos R, tan Q |
|
△ ABC is right angle triangle at A, AB=11, BC=13, AC=8. Write sin A, cos C, tan A |
|
△ PQR is right angle triangle at Q, PQ=7, QR=9, PR=11. Write sin R, cos R, tan P |
|
△ ABC is right angle triangle at B, AB=11, BC=9, AC=17. Write sin A, cos C, tan C |
|
△ PQR is right angle triangle at Q, PQ=13, QR=7, PR=19. Write sin R, cos P, tan P |
|
If cos Θ = 11/13, find sin Θ and tan Θ |
|
If sin Θ = 7/11, find cos Θ and tan Θ |
|
If cos Theta = 2/3, find sin and tan theta |
|
If Tan Θ = 3/5, find sin Θ and cos Θ |
|
△ ABC is right angle triangle at B, AB=8, BC=11, AC=13. Write Cosec C, Sec A, Cot C |
|
If Sin Θ = 5/7, find cos Θ and tan Θ |
|
If Tan Θ = 2/3, find Sin Θ and Cos Θ |
|
△ ABC is right angle triangle at A, AB=11, BC=13, AC=8. Write Cosec A, Sec C, Cot A |
|
△ PQR is right angle triangle at P, PQ=9, QR=11, RP=7. Write Cosec Q, Sec R, Cot Q |
|
△ PQR is right angle triangle at Q, PQ=7, QR=9, PR=11. Write Cosec R, Sec R, Cot P |
|
△ ABC is right angle triangle at B, AB=11, BC=9, AC=17. Write Cosec A, Sec C, Cot C |
|
△ PQR is right angle triangle at Q, PQ=13, QR=7, PR=19. Write Cosec R, Sec P, Cot P |
|
If Sec Θ = 11/13, find Cosec Θ and Cot Θ |
|
If Cosec Θ = 7/11, find Sec Θ and Cot Θ |
|
If Cot Θ = 3/5, find Cosec Θ and Sec Θ |
|
If Sec Θ = 2/3, find Cosec Θ and Cot Θ |
|
If Cosec Θ = 5/7, find Sec Θ and Cot Θ |
|
If Cot Θ = 2/3, find Cosec Θ and Sec Θ |
|






