In the following diagram:
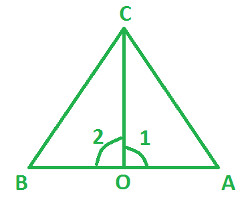
CO is a bisector of ∠ AOB
∠ 1 = ∠ 2
Prove △ OBC ≅ △ OAC |
In the given triangle:

∠ BCO = ∠ ACO (CO is a bisector of ∠ AOB)
∠ 1 = ∠ 2 (given)
CO = CO (common side)
Therefore, ASA rule of congruence applies here and we get following corresponding relationships:
A ↔ B
O ↔ O
C ↔ C
Hence, △ OBC ≅ △ OAC
|
Related Question Examples
In the following diagram:

CO is a bisector of ∠ AOB
∠ 1 = ∠ 2
Prove △ OBC ≅ △ OAC |
In the following diagram:

∠ QPS = ∠ PQR
∠ PQS = ∠ QPR
Prove △ SPQ ≅ △ RQP |
In the following diagram:
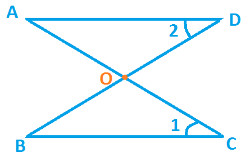
DO = CO
∠ 1 = ∠ 2
Prove △ AOD ≅ △ BOC |
|






