Angle Sum Property of Triangle : Solved Examples

Sum of Two Sides	Angle Sum Property	Angles opposite to equal sides of triangle are equal	Angle opposite to longer side is greater	Pythagoras Theorem
Exterior Angle Property of a Triangle	Mid point property of Triangle	Triangles on same base & between same parallel lines

Find the measurement of ∠ A in the following figure: 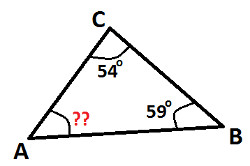In the given triangle: ∠ C = 54 ∠ B = 59 Apply angle sum property of triangle and we get ∠ A + ∠ B + ∠ C = 180° Put the values of ∠ C & ∠ B from above and we get: ∠ A + 54° + 59° = 180° Solve L.H.S. addition expression and we get: ∠ A + 113° = 180° Subtract 113 from both sides and we get: ∠ A = 67° Hence, measurement of ∠ A in given triangle is 67° Related Question Examples Find the measurement of ∠ A in the following figure: In a triangle PQR, ∠ P is equals to 50° and ∠ Q & ∠ R are equal. Find measurement of ∠ Q & ∠ R Angles of a triangle are in the ratio of 1:2:1. Find the measurement of all the angles.