Before you learn how to divide a decimal (whose whole number part is zero) with a whole number; you must be aware of the whole number part and fractional part of decimal and you can study this from:
Define Decimal
Also, you are advice to study:
Define Multiples
Convert Decimal into Fraction
Convert Proper Fraction into Decimal
Place Value of Digits in Decimal
Multiplicative Inverse
Define Dividend
Define Divisor
Define Quotient
Define Remainder
There are three methods for divisions:
Method 1: Division of the fractional part of decimal.
E.g. Divide 0.9 by 3 with the help of Method 1:
= 0.9 ÷ 3
Now, we know that 9 is at tenths place; we can write the division as:
= 9 tenths ÷ 3
Divide 9 by 3 and we get:
= 3 tenths
Now, 3 tenths can be converted into decimal form again and we get:
= 0.3
Method 2: Cross Multiplication Method
E.g. Divide 0.9 by 3 with the help of Method 2:
= 0.9 ÷ 3
Convert decimal into fraction and we get:
Multiply the resultant fraction with the multiplicative inverse of divisor and we get:
Solve by Cross multiplication and we get:
On solving the above expression, we get:
Convert the above proper fraction into decimal and we get:
= 0.3
Method 3: Long division method.
E.g. Divide 0.135 by 5 using Method 3:
= 0.135 ÷ 5
Place dividend and divisor in long division method, as shown below
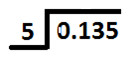
Since fractional part of decimal in dividend is zero, so we will write Zero at ones place in quotient and then place decimal point; as shown below:
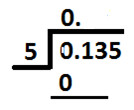
Now, divide digit at tenths place (1) by divisor (5).
As 1 is less than 5, we will write Zero at tenths place in quotient as shown below:
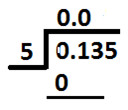
Now, we will take digit at tenths place & hundredths place and divide them collectively by divisor (5), as shown below:
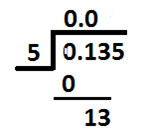
Since 13 is not exactly divisible by 5, so we will choose a multiple of 5 which is nearest to 13.
And Nearest number to 13 which is also a multiple of 5 = 10
Place 10 below 13 as shown below:
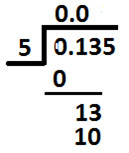
Now, 10 which is a multiple of 5 and on dividing 10 by 5 we get 2.
So, we write 2 at hundredths place in the quotient (as shown below):
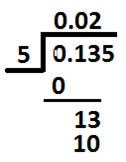
Subtract 10 from 13 and we get 3 as remainder.
Write remainder as shown below:
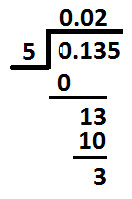
Now, place 5 (which is at thousandths place in dividend) next to remainder 3 (calculated above) as shown below:
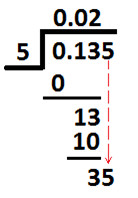
Now, divide 35 (shown above) by divisor 5 & we get 7
So, write 7 at thousandths place in the quotient and we get:
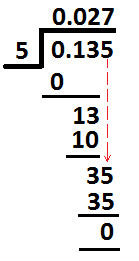
Subtract 35 from 35 and we get Zero as remainder.
So, this is the end of long division method and we get:
0.135 ÷ 5 = 0.027
|






