Construct a triangle PQR, where Angle QPR = 90 degree, PQ = 6 cm and RQ = 7cm
Step of construction of Right Angled Triangle, whose length of hypotenuse and one side are given:
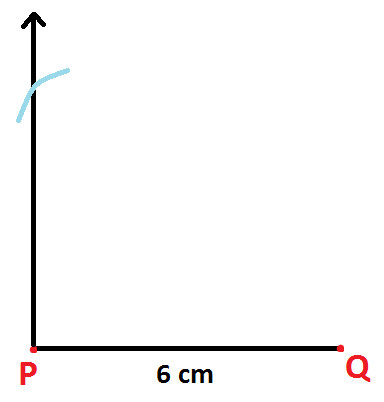
Step 1: Use ruler and draw a line segment PQ of 6cm (as shown below):

Step 2: Use protractor and draw angle of 90 degree at point P (as shown below):

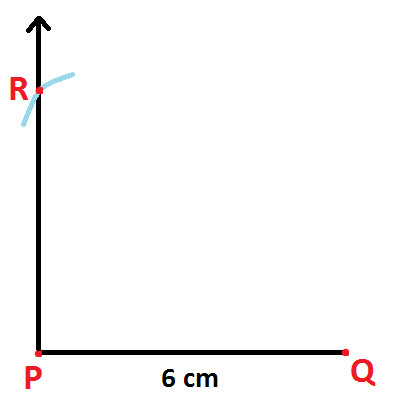
Step 3: Use compass and 7 cm wide open. With Q as center, draw and arc with cut arm of 90 degree angle drawn in step 2 (as shown below)
Step 4: Mark point of intersection as point R (as shown below):
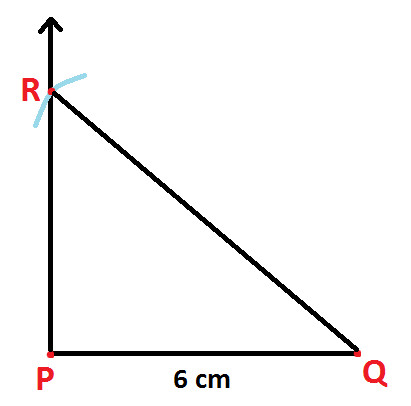
Step 5: Join points R and Q (as shown below)
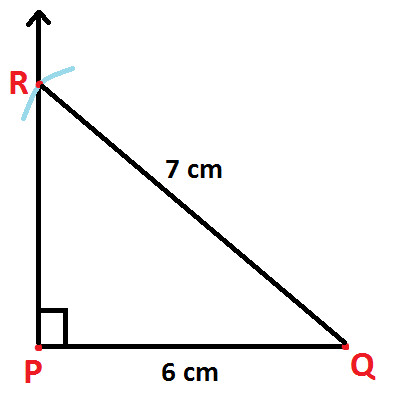
Step 6: Use rule and check the length of RQ and it has to be of length 7cm. And we get the resultant Right Angled Triangle PQR (as shown below)
|






