Before you study this topic; you are adviced to study
Define Congruence / Congruent
Congruent Triangles
Corresponding Parts of Congruent Triangles
ASA rule of Congruence illustrates that, if two angles and its included side are equal to the two corresponding sides and the included side of another triangle; then both the triangle are said to be congruent.
Example 1: In the following diagram:
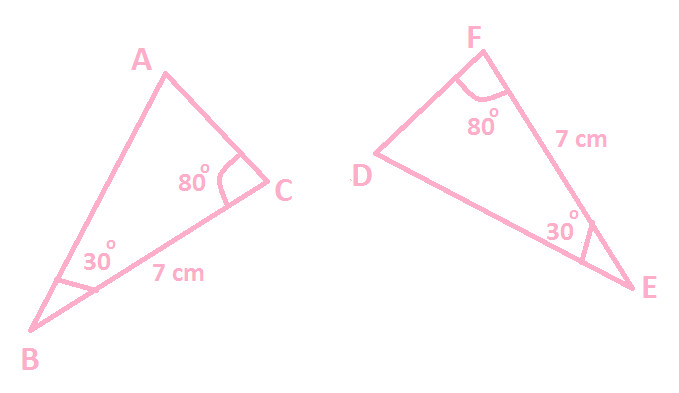
Prove △ ABC ≅ △ DEF
Solution: In the given diagram:
BC = EF (7 cm each)
∠ B = ∠ E (30 Degree each)
∠ C= ∠ F (80 Degree each)
We can observe that:
Two angles (∠ B & ∠ C) of △ ABC are equal to corresponding two angles (∠ E & ∠ F) of △ DEF.
Side BC (included side to ∠ B & ∠ C) of ∆ ABC is equal to side EF (included side to ∠ E & ∠ F) of △ DEF
Therefore, from the above two observations, ASA congruence rules apply and we can say △ ABC and △ DEF are congruent.
And the corresponding relationships are as:
A ↔ D
B ↔ E
C ↔ F
Hence, △ ABC ≅ △ DEF
Example 2: In the following diagram:

Prove △ ABC ≅ △ DEF
Solution: In the given diagram:
AC = DF (7 cm each)
∠ B = ∠ E (30 Degree each)
∠ C= ∠ F (80 Degree each)
We can observe that:
Two angles (∠ B & ∠ C) of △ ABC are equal to corresponding two angles (∠ E & ∠ F) of △ DEF.
Side AC of △ ABC is equal to side DF of △ DEF
In the above 2nd observation, you can notice that sides AC & DF are not included side to ∠ B & ∠ C of △ ABC and to ∠ E & ∠ F of △ DEF respectively.
Therefore, SAS congruence rule fails to apply here and we get:
Hence, △ ABC not congruent △ DEF
Justification / Proof - ASA Congruence Rule
Now, let's justify or proof of ASA Rule of Congruence with the help of following three checks:
Check 1:
There is a given triangle XYZ and measure of one of its ∠ X is equal to 60. You are asked to construct a triangle ABC congruent to triangle XYZ.
Can you do that ??
With measure of one of its angle is given i.e. 60, following triangles can be formed:
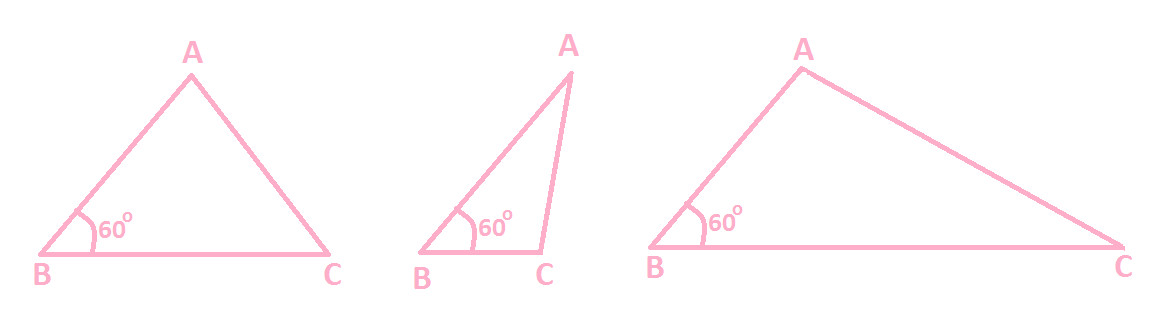
From the above diagram of triangles, you can observe that given triangle XYZ can be any of the following and we are not sure which diagram of triangle is congruent to Triangle XYZ.
Hence, this confirms that two triangles cannot be congruent, if one angle of a triangle is equal to the corresponding one angle of another triangle.
Check 2:
There is a given triangle XYZ , XY = 7cm & ∠ X = 60
Can you construct a triangle ABC congruent to triangle XYZ ?
With length of one side 7 cm & measure of one angle 60, we can construct many triangles:
(for instance)
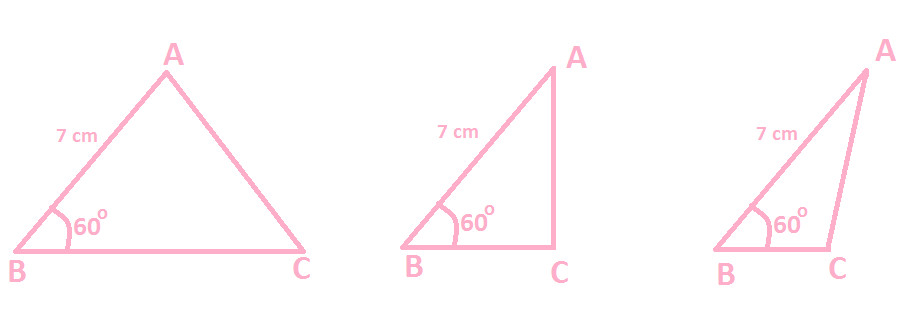
From the above diagram of different triangles, you can observe that given triangle XYZ can be any of the following and we are not sure which diagram of Triangle ABC is congruent to Triangle XYZ.
Hence, this confirms that two triangles cannot be congruent, if one sides and one angle of a triangle are equal to the two corresponding sides and one corresponding angle of another triangle.
Check 3:
There is a given triangle XYZ , where XY = 7 cm, ∠ X = 45 & ∠ Y = 60Can you construct a triangle ABC congruent to triangle XYZ ?
Let's try to construct a triangle ABC congruent to triangle XYZ, when measure of two angles and length of one side are given.
Steps of construction are as follows:
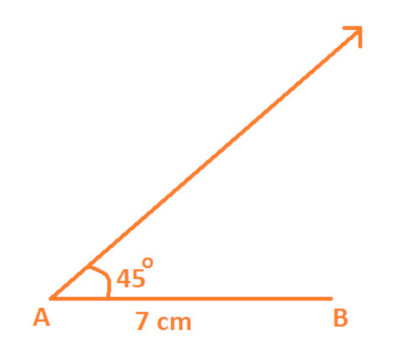
Step 1: Draw a line segment AB with length 5 cm, as shown in the below diagram:
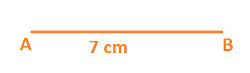
Step 2: With the help of protractor and with A as center draw an angle of 45 and extend its arc to any convenient length, as shown below:
Step 3: Now, again with the help of protractor and with B as center; draw an angles of 60 which intersects with arm of ∠ A at point C, as shown below:
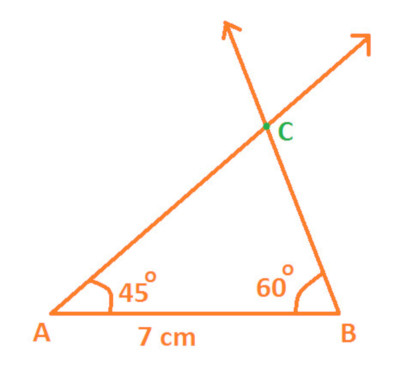
Therefore resultant figure is a △ ABC with:
AB = 7 cm
∠ B = 60 °
∠ A = 45 °
Now you can see that:
AB XY (7 cm each)
∠ B ∠ Y (60 each)
∠ A ∠ X (45 each)
So, on the basis above correspondence we get:
△ ABC ≅ △ XYZ
Hence, this proves ASA rule of Congruence which says:
"If two angles and its included side are equal to the two corresponding sides and the included side of another triangle; then both the triangle are said to be congruent"
Study More Solved Questions / Examples
In the following diagram:
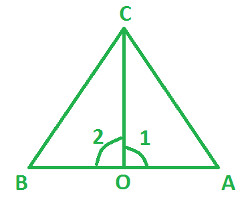
CO is a bisector of ∠ AOB
∠ 1 = ∠ 2
Prove △ OBC ≅ △ OAC |
In the following diagram:

∠ QPS = ∠ PQR
∠ PQS = ∠ QPR
Prove △ SPQ ≅ △ RQP |
In the following diagram:
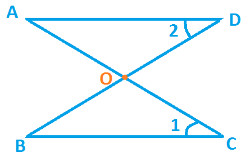
DO = CO
∠ 1 = ∠ 2
Prove △ AOD ≅ △ BOC |
| | |






