Area of Triangle

Properties	Types / Classification	Perimeter of Equilateral Triangle	Median of Triangle	Interior of a Triangle
Exterior of a Triangle	Altitude of a Triangle	Interior Angles of Triangle	Exterior Angles of Triangle	Interior Opposite Angles of Triangle
Adjacent Interior Angle of Triangle	Congruent Triangles	Area of Triangle	Area of Triangle by Heron's Formula	Construction of Triangle (compass)

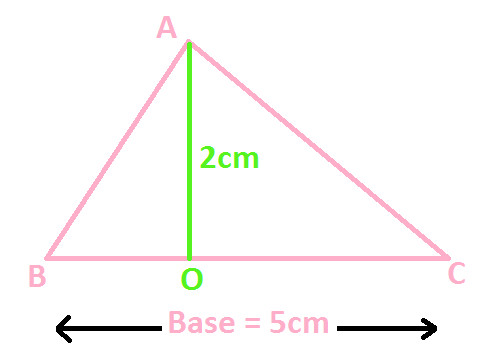
Before you understand how to find area of triangle, you are advised to read: What is Parallelogram ? How to find Area of a Parallelogram ? Formula for Area of Triangle = 1/2 X Base X Altitude In the following diagram of Triangle ABC: Three sides are AB, BC and AC Base = BC = 5cm Altitude or Height = AO = 2cm Now, find area of triangle with the help of above formula and we get: Area of Triangle = 1/2 X Base X Altitude Put the values of base and altitude from above and we get: Area of Triangle = 1/2 X (5 X 2) Area of Triangle = 1/2 X (10) Area of Triangle = 1/2 X 10 Area of Triangle ABC = 5cm2 Let's prove the formula for Triangle and understand how we got the area of triangle. 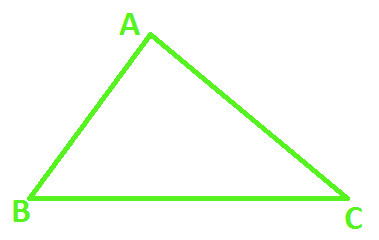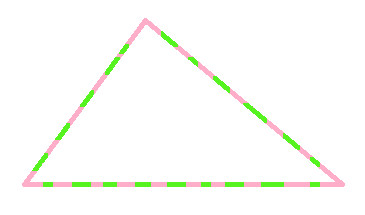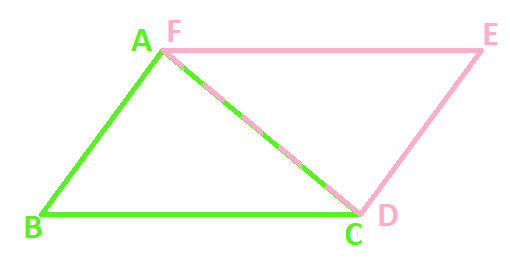Let's take a triangle ABC with sides of any dimensions (as shown below) Now construct another triangle DEF with same dimensions (as shown below) Superpose one triangle over the other, to check whether they perfectly match (as shown below) Now, since both are of perfect match, join the corresponding sides of both the triangles (as shown below) In above diagram, you can observe that sides AC and DF coincide with each other and we get the following resultant quadrilateral ABCE: 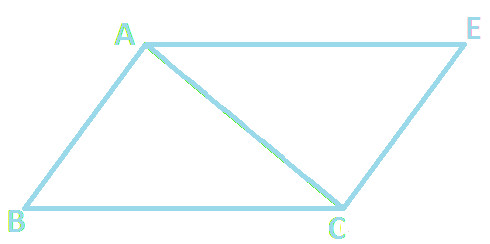Above Quadrilateral ABCE having sides AB, BC, CE and AE Quadrilateral ABCE is formed by joining together two equal Triangles i.e △ ABC and △ DEF (as shown below) 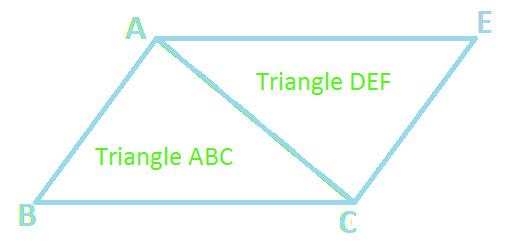Therefore we can say that: Area of Quadrilateral ABCE = Area of △ ABC + Area of △ DEF ..... 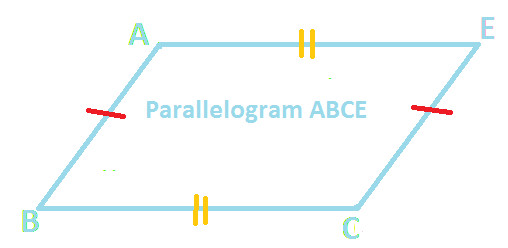(Statement 1) Also, on observing the quadrilateral ABCE (as shown below): AB // CE BC // AE AB = CE (corresponding equal sides of equal triangles) BC = AE (corresponding equal sides of equal triangles) Hence, Quadrilateral ABCE is a parallelogram ..... (Statement 2) From Statement 1 and 2, we get: Area of Parallelogram ABCE = Area of △ ABC + Area of △ DEF Now, we know that △ ABC = △ DEF so we get: Area of Parallelogram ABCE = Area of ABC + Area of ABC Or we can write it as: Area of Parallelogram ABCE = 2 (Area of △ ABC) Now apply the formula for area of parallelogram and we get: Base X altitude = 2 (Area of △ ABC) Divide both sides by 2 and we get: 1/2 X Base X Altitude = Area of ABC Or we can write it as: Area of △ ABC = 1/2 X Base X Altitude Therefore, Area of △ ABC = Area of △ DEF = 1/2 X Base X Altitude (because △ ABC = △ DEF) Hence, this proves the formula for Area of Triangle i.e. Area of Triangle = 1/2 X Base X Altitude You can try this with different triangle having different dimensions of side, but you will notice the same result.