Angle Sum Property of a Triangle says that Sum of all the Angles of the Triangle is always equal to 180°.
For Better understanding of Angle Sum Property, study the following examples :-
Example 1 = Below diagram represent Triangle ABC
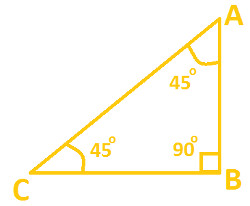
In the above diagram, Triangle ABC has
∠ A = 45°
∠ B = 90°
∠ C = 45°
Now as per the Angle Sum Property,
Sum of ∠ A, ∠ B & ∠ C has to be equal to 180°.
Lets Check the property :-
∠ A + ∠ B + ∠ C = 180°
Put the values of all angle and we get:
45° + 90° + 45° = 180°
180° = 180°
since L.H.S = R.H.S
Hence its proved that Sum of all the Angles of the Triangle is always equal to 180°.
Example 2 = Below diagram represent Triangle PQR
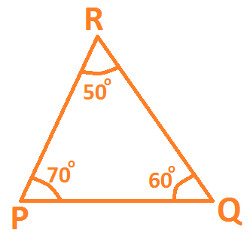
In the above diagram, Triangle ABC has
∠ P = 70°
∠ Q = 60°
∠ R = 50°
Now as per the Angle Sum Property,
Sum of ∠ P, ∠ Q & ∠ R has to be equal to 180°.
Lets Check the property :-
∠ P + ∠ Q + ∠ R = 180°
Put the values of all angle and we get:
70° + 60° + 50° = 180°
180° = 180°
since L.H.S = R.H.S
Hence its proved that Sum of all the Angles of the Triangle is always equal to 180°.
How to prove angle sum property of triangle:
There are several methods to prove angles sum property of triangle, but here we have explained three methods only.
Method 1: Prove angle sum property of triangle with the help of protractor
Draw a triangle and measure all its angles with the help of protractor.
Now add the measurement and you will notice that sum of these measurement is equal to 180° (ignore marginal error).
You can try this with few more triangles and you will notice that in all other triangles too; sum of measurement of all the angles is equal to 180°.
Hence, this prove angles sum property of triangle, which says that sum of all the angles of triangle is equals to 180°
Method 2: Prove angle sum property of triangle with the help of exterior angle property.
Before you study this method you are advised to read:
What is Exterior Angle Property of a Triangle ?
What is Linear Pair ?
Draw a triangle ABC and produce BC to D as shown in the following figure:
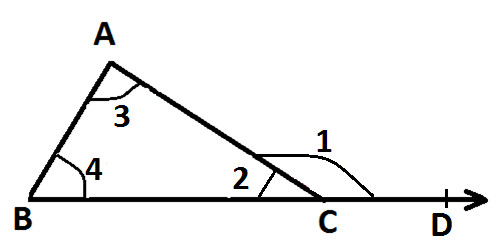
Mark all the angles of triangles as ∠ 2, ∠ 3 & ∠ 4 as shown in the above figure.
Also, mark exterior angle as ∠ 1 as shown in the above figure.
Now as per Exterior Angle Property which says that exterior angle is equal to sum of interior opposite angles; we get:
∠ 1 = ∠ 4 + ∠ 3 .....(statement 1)
Also, ∠ 1 & ∠ 2 from linear pair, so we get:
∠ 1 + ∠ 2 = 180°
Put the Values of angles ∠ 1 from (statement 1) and we get:
∠ 4 + ∠ 3 + ∠ 2 = 180°
And ∠ 4, ∠ 3 & ∠ 2 all are the angles of triangle ABC.
Hence, Angle Sum Property is proved which says that Sum of all the angles of a triangle are equals to 180°
Method 3: Prove angle sum property of triangle with the principles of parallel lines cut by a transversal
Before you understand this method, you are advised to read:
What is Transversal Line ?
What are the Properties of Transversal ?
What is Linear Pair ?
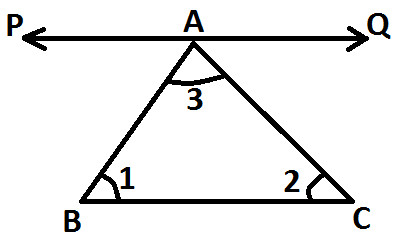
In the below diagram we have a triangle ABC and we have to prove the angle sum property of triangle i.e. sum of it's angles is equal to 180°
Or we write it as:
∠ 1 + ∠ 2 + ∠ 3 = 180°
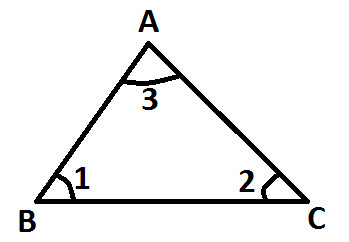
Following are the steps to prove Angle Sum Property of Triangle:
Draw a line PQ parallel to side BC which passes through the Vertex A (as shown below):
Line PQ is parallel to BC and AB is a transversal, we get:
∠ 1 and ∠ 4 are alternative interior (as shown below)

And as per the property of transversal, If two parallel lines are cut by a transversal, then pair of alternative interior angles are equal. So we get:
∠ 1 = ∠ 4 ..... (Statement 1)
Similarly, Line PQ is parallel to BC and AC is a transversal, we get:
∠ 2 and ∠ 5 are alternative interior angles (as shown below):
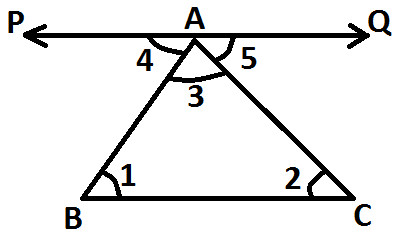
And as per the property of transversal, "If two parallel lines are cut by a transversal, then pair of alternative interior angles are equal". So we get:
∠ 2 = ∠ 5 ..... (Statement 2)
Now, you can observe that Angle 3, Angle 4 and Angle 5 lies on the line PQ, thereby forming a Linear Pair, so we get:
∠ 4 + ∠ 3 +∠ 5 = 180°
As proved in statement 1 and 2 above (∠ 4 = ∠ 1 & ∠ 5 = ∠ 2), so we get:
∠ 1 + ∠ 3 + ∠ 2 = 180°
Or we can write it as:
∠ 1 + ∠ 2 + ∠ 3 = 180°
Hence, this proved angle sum property of triangle with the principles of parallel lines cut by a transversal
Study More Solved Questions / Examples
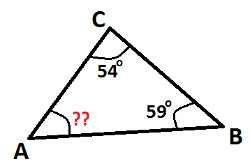
Find the measurement of ∠ A in the following figure:
 |
|
In a triangle PQR, ∠ P is equals to 50° and ∠ Q & ∠ R are equal. Find measurement of ∠ Q & ∠ R |
|
Angles of a triangle are in the ratio of 1:2:1. Find the measurement of all the angles. |
| | |






