Define :Trigonometry - The word Trigonometry is derived and made up of three Greek words tri(which means three), gon (which means sides) and metron (which means measure). The symbol we used for theta is Θ
It is in-fact a study of relationships between the sides and angles of a triangle.
First we will start with what is Theta Angle and how to write Sin Θ, Cos Θ and Tan Θ ratios
Lets draw an acute angle as mentioned below

Now we will draw a perpendicular PB on line AY, AX
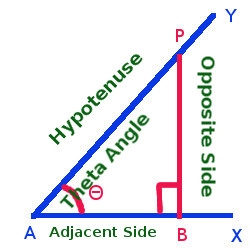
We get the following by drawing this perpendicular
A right angle is formed △ PAB in which ∠ PAB = Θ
PB is opposite to ∠ Θ and is called opposite side
AB is the adjacent side to ∠ Θ
AP is hypotenuse
so Sin Θ, Cos Θ and Tan Θ will be as follows -
Sin Θ = PB/AP = Opposite Side/Hypotenuse (The ratio PB/AP is called Sine of angle Θ)
Cos Θ = AB/AP = Adjacent Side/Hypotenuse (The ratio AB/AP is called cosine of angle Θ)
Tan Θ = PB/AB = Opposite Side/Adjacent Side (The ratio PB/AB is called Tangent of angle Θ)
Lets study some examples on how to write Sin Θ, Cos Θ and Tan Θ
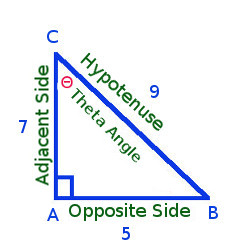
Example 1 - △ ABC is right angle triangle at A, AB=5, AC=7, BC=9. write sin B, cos B, tan B
Solution - Lets draw the right angle triangle with the above mentioned details
Given thing are
Right angle at A
Theta Angle at B (As mentioned in example statement sin B, Cos B, tan B that means angle B should be taken as Theta)

Hypotenuse : BC = 9
Opposite Side : AC = 7
Adjacent Side : AB = 5
Sin B = Opposite Side/Hypotenuse = 7/9
Cos B = Adjacent Side/Hypotenuse = 5/9
Tan B = Opposite Side/Adjacent Side = 7/5
Lets twist the above example 1 statement and change the theta angle of Cos
Example 2 - △ ABC is right angle triangle at A, AB=5, AC=7, BC=9 write sin B, cos C, tan B
Solution - Lets draw the right angle triangle with the above mentioned details
Given thing are
Right angle at A
Theta Angle at B (As mentioned in statement sin B, tan B that means angle B should be taken as Theta)

Hypotenuse : BC = 9
Opposite Side : AC = 7
Adjacent Side : AB = 5
Sin B = Opposite Side/Hypotenuse = 7/9
Tan B = Opposite Side/Adjacent Side = 7/5
For Cos the Theta Angle is at C (As mentioned in statement "Cos C" that means angle C should be taken as Theta)
As cos angle is now C, the adjacent side and opposite side of the triangle will be as below
You will see that Theta angle is now at C, So
Hypotenuse : BC = 9
Opposite Side : AC = 5
Adjacent Side : AB = 7
So, cos C = Adjacent Side/Hypotenuse = 7/9
Now, we will learn how to write Cosec Θ, Sec Θ and Cot Θ ratios
As you already know how to write Sin Θ, Cos Θ and Tan Θ, the reciprocal of these ratios will become Cosec Θ, Sec Θ and Cot Θ and these are defined as follows -
Cosec Θ = Hypotenuse / Opposite Side
Sec Θ = Hypotenuse / Adjacent Side
Cot Θ = Adjacent Side / Opposite Side
Lets study some examples on how to write Cosec Θ, Sec Θ and Cot Θ
Example 3 - △ ABC is right angle triangle at A, AB=5, AC=7, BC=9. write Cosec B, Sec B, Cot B
Solution - Lets draw the right angle triangle with the above mentioned details
Given thing are
Right angle at A
Theta Angle at B (As mentioned in example statement Cosec B, Sec B, Cot B that means angle B should be taken as Theta)

Hypotenuse : BC = 9
Opposite Side : AC = 7
Adjacent Side : AB = 5
Cosec B = Hypotenuse / Opposite Side = 9/7
Sec B = Hypotenuse / Adjacent Side = 9/5
CotB = Adjacent Side / Opposite Side = 5/7
Lets twist the above example 3 statement and change the theta angle of Sec
Example 4 - △ ABC is right angle triangle at A, AB=5, AC=7, BC=9 write Cosec B, Sec C, Cot B
Solution - Lets draw the right angle triangle with the above mentioned details
Given thing are
Right angle at A
Theta Angle at B (As mentioned in statement Cosec B, Cot B that means angle B should be taken as Theta)

Hypotenuse : BC = 9
Opposite Side : AC = 7
Adjacent Side : AB = 5
Cosec B = Hypotenuse / Opposite Side = 9/7
Cot B = Adjacent Side / Opposite Side = 5/7
For Sec the Theta Angle is at C (As mentioned in statement "Sec C" that means angle C should be taken as Theta)
As Sec angle is now C, the adjacent side and opposite side of the triangle will be as below

You will see that Theta angle is now at C, So
Hypotenuse : BC = 9
Opposite Side : AC = 5
Adjacent Side : AB = 7
So, cos C = Hypotenuse / Adjacent Side = 9/7
Study More Solved Questions / Examples
|
△ ABC is right angle triangle at B, AB=8, BC=11, AC=13. Write sin C, cos A, tan C |
|
△ PQR is right angle triangle at P, PQ=9, QR=11, RP=7. Write sin Q, cos R, tan Q |
|
△ ABC is right angle triangle at A, AB=11, BC=13, AC=8. Write sin A, cos C, tan A |
|
△ PQR is right angle triangle at Q, PQ=7, QR=9, PR=11. Write sin R, cos R, tan P |
|
△ ABC is right angle triangle at B, AB=11, BC=9, AC=17. Write sin A, cos C, tan C |
|
△ PQR is right angle triangle at Q, PQ=13, QR=7, PR=19. Write sin R, cos P, tan P |
|
If cos Θ = 11/13, find sin Θ and tan Θ |
|
If sin Θ = 7/11, find cos Θ and tan Θ |
|
If cos Theta = 2/3, find sin and tan theta |
|
If Tan Θ = 3/5, find sin Θ and cos Θ |
|
△ ABC is right angle triangle at B, AB=8, BC=11, AC=13. Write Cosec C, Sec A, Cot C |
|
If Sin Θ = 5/7, find cos Θ and tan Θ |
|
If Tan Θ = 2/3, find Sin Θ and Cos Θ |
|
△ ABC is right angle triangle at A, AB=11, BC=13, AC=8. Write Cosec A, Sec C, Cot A |
|
△ PQR is right angle triangle at P, PQ=9, QR=11, RP=7. Write Cosec Q, Sec R, Cot Q |
|
△ PQR is right angle triangle at Q, PQ=7, QR=9, PR=11. Write Cosec R, Sec R, Cot P |
|
△ ABC is right angle triangle at B, AB=11, BC=9, AC=17. Write Cosec A, Sec C, Cot C |
|
△ PQR is right angle triangle at Q, PQ=13, QR=7, PR=19. Write Cosec R, Sec P, Cot P |
|
If Sec Θ = 11/13, find Cosec Θ and Cot Θ |
|
If Cosec Θ = 7/11, find Sec Θ and Cot Θ |
|
If Cot Θ = 3/5, find Cosec Θ and Sec Θ |
|
If Sec Θ = 2/3, find Cosec Θ and Cot Θ |
|
If Cosec Θ = 5/7, find Sec Θ and Cot Θ |
|
If Cot Θ = 2/3, find Cosec Θ and Sec Θ |
| | |






