Before you understand this topic, you are advised to read:
What is Parallelogram ?
What are Parallel Lines ?
What are Congruent figures ?
What are the rules of Congruent Triangle ?
What are Transversal Lines ?
What are Corresponding Angles ?
What is Angle Sum Property of Triangle ?
This is one of the properties of triangle which says Triangles on the same base and between same parallel lines are equal in area
Let's first understand how this situation looks like
Observe the following diagram having two triangles - △ ABC and △ BCD

Observe carefully and you can notice that in the above diagram there are two triangles (as shown below):
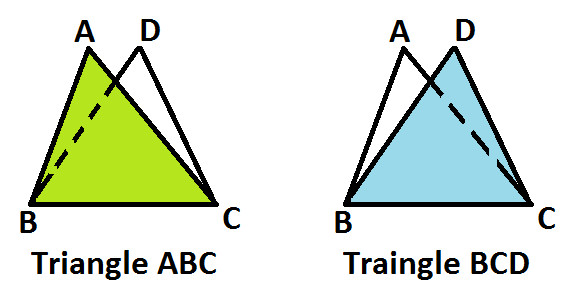
Also, you can notice that both the triangle ABC and BCD are on the same base BC (as shown below)
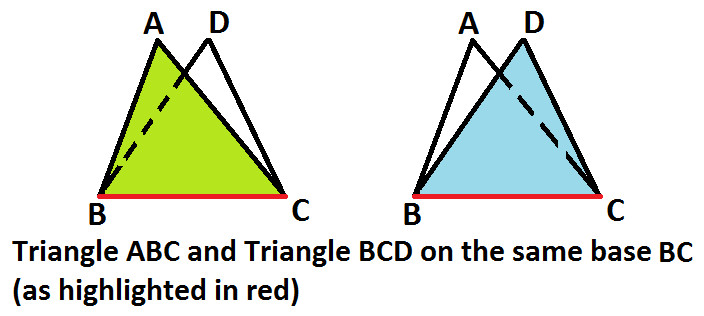
Now, if you join vertices A & D with a line XY, you will notice that BC is parallel to XY.
And both the triangles ABC and BCD are between same parallel lines BC and XY (as shown below)
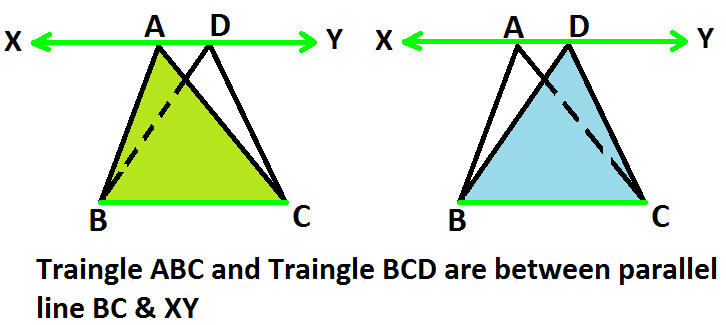
Hence, you can see how triangles can be on same base and between same parallel lines.
Now, let's prove this property that areas of triangles on the same base and between same parallel lines are same. i.e.
Area of △ ABC = Area of △ BCD
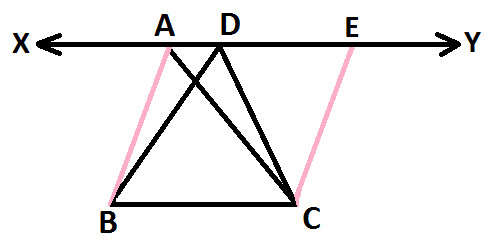
Observe the following diagram:

Join vertices A & D with a line XY, you will notice that BC is parallel to XY (as shown below):
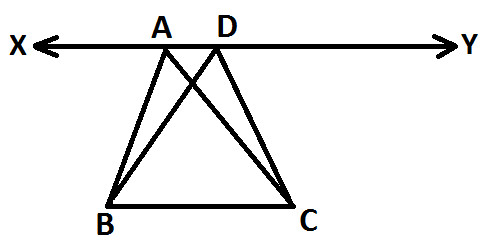
From Vertex C, draw a line parallel to AB which meets line XY at point E and we get:
AB is parallel to CE (as shown below)
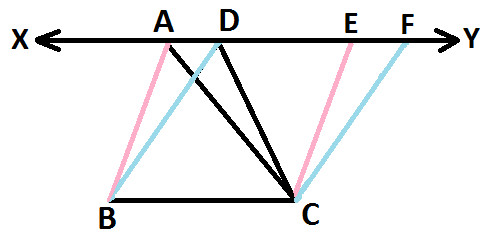
From Vertex C, draw another line parallel to BD which meets line XY at point F and we get:
BD is parallel to CF (as shown below)
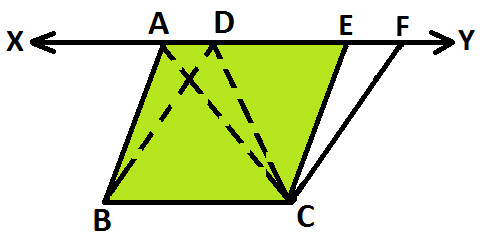
Since XY is parallel to BC and AB is parallel to CE, so we get:
Parallelogram ABCE (as shown below):
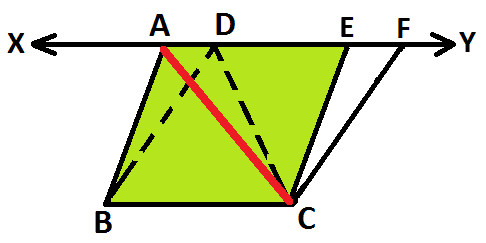
In parallelogram ABCE, AC is a diagonal (as highlighted in red in below diagram):
Now, as we know that:
Diagonals of a Parallelogram, divides it into two congruent triangles ( Diagonals of a parallelogram divide it into two congruent triangles )
So, we have △ ABC ≅ △ ACE (as shown below):
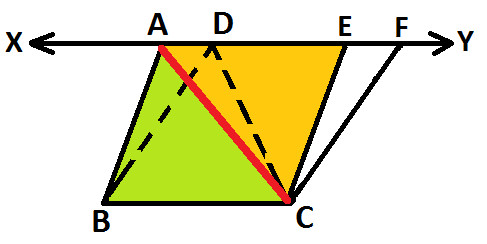
Since, we know that congruent figures are equal in area, so we get:
Area of △ ABC = Area of △ ACE ..... (statement 1)
Now we know that:
Area of Parallelogram ABCE = Area of △ ABC + Area of △ ACE
From Statement 1:
Area of △ ABC = Area of △ ACE, so we get:
Area of Parallelogram ABCE = Area of △ ABC + Area of △ ABC
Solve L.H.S and we get:
Area of Parallelogram ABCE = 2 Area of △ ABC ..... (statement 2)
Similarly, since XY is parallel to BC and BD is parallel to CF, so we get:
Parallelogram BDFC (as shown below):

In parallelogram BDFC, DC is a diagonal (as highlighted in red in below diagram):
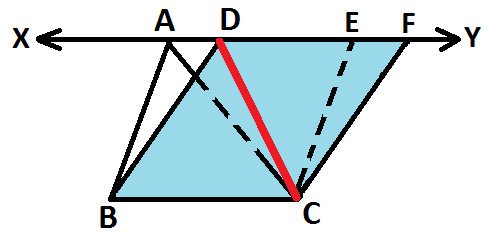
Now, as we know that:
Diagonals of a Parallelogram, divides it into two congruent triangles ( Diagonals of a parallelogram divide it into two congruent triangles )
So, we have △ BCD ≅ △ DCF (as shown below):
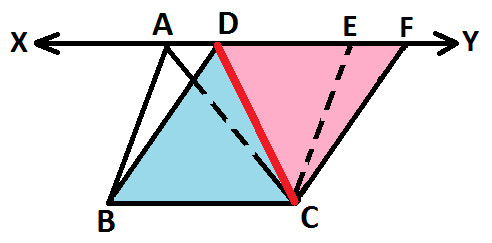
Since, we know that congruent figures are equal in area, so we get:
Area of △ BCD = Area of △ DCF ..... (statement 3)
Now we know that:
Area of Parallelogram BDFC = Area of △ BCD + Area of △ DCF
From Statement 1:
Area of △ BCD = Area of △ DCF, so we get:
Area of Parallelogram ABCE = Area of △ BCD + Area of △ BCD
Solve L.H.S and we get:
Area of Parallelogram ABCE = 2 Area of △ BCD ..... (statement 4)
Now, you can also observe that
Parallelogram ABCE and Parallelogram BDFC are between same base BC and between same parallel lines BC and XY (as shown below):
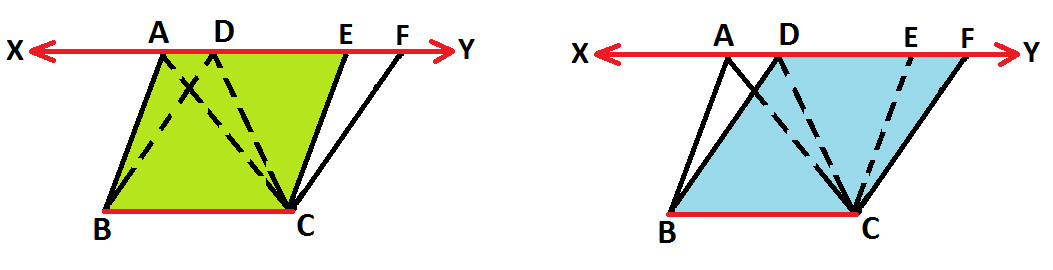
Here we applied the property of Parallelogram that:
Parallelograms on the same base between same parallel lines are equal in areas and we get: ( Parallelogram on the same base and between same parallel lines )
Area of Parallelogram ABCE = Area of Parallelogram BDCF
In statement 2 and 4 above we proved that:
Area of Parallelogram ABCE = 2 Area of △ ABC
Area of Parallelogram BDFC = 2 Area of △ BCD
So replacing these values we get:
2 Area of △ ABC = 2 Area of △ BCD
Dividing both side by 2 and we get:
Area of △ ABC = Area of △ BCD (as shown below):
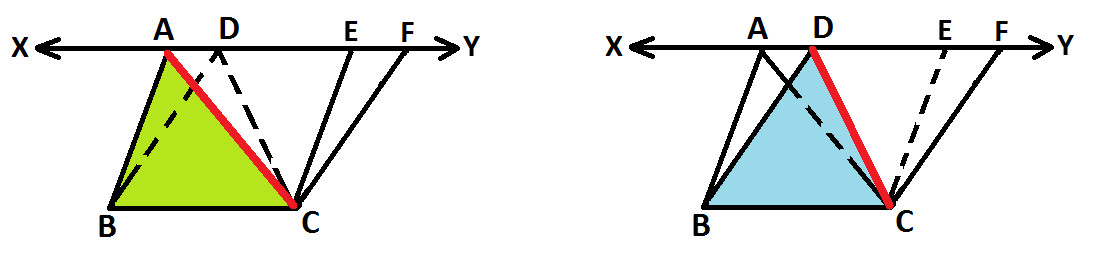
This is how this property of triangle is obtained.
From this property, we get the converse of this property which also stand true:
Two Triangles on the same base and equal in areas lie between the same parallel lines
|






