Definition
The term Percentage was derived from two Latin Words Per and Centum which means Out of Hundred.
Percentage is denoted by a symbol ' % '.
Percentage compares between the whole and its parts.
Before you understand, how Percentage compare between the whole and its parts; lets understand what is whole and what are its parts ?
Observe the following diagram; illustrating Whole and Its Parts
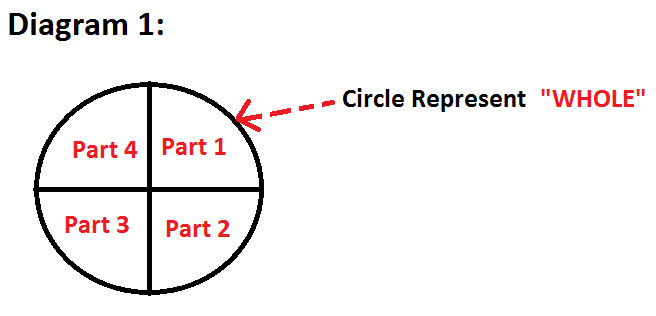
As you can observe in diagram 1:
Whole is represented in the form of Circle.
Part 1, Part 2, Part 3, Part 4 represents different parts of the whole
Or we can also write it as:
Whole Circle = Part 1 + Part 2 + Part 3 + Part 4
This means that sum of all the parts is equal to the whole or we can say that value of whole part is equal to the sum of values of all its part
Now let's understand this whole and its parts from a real life example:
Example: Four friends ordered a pizza. Pizza was divided into four equal portions. And each friend ate one portion.
Now in this situation:
Pizza represents the whole and four portions represent its 4 equal parts.
Now let's understand the significance of Percentage, which helps to find the value of the whole and its parts:
Value of whole part is always 100%
And as explained above, whole part is equal to sum of all parts; so:
This 100% value of whole part in divided into its different parts.
Observe the following diagram 2 & 3:
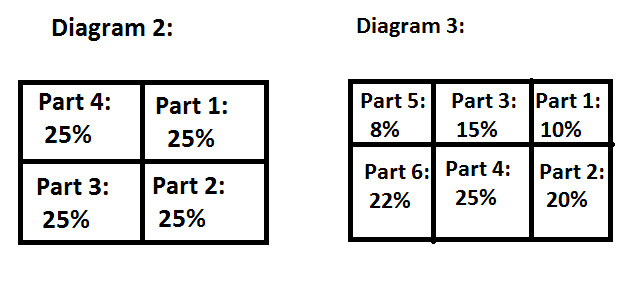
Following are the observation from diagram 2 & 3:
Value of whole in both the diagram is same i.e. 100%
Sum of the values of parts in both the diagram is equal to 100% which is the value of whole
Number of parts of a whole is not definite and it can vary from situation to situation
Values of parts of the whole can be same as well as different also.
Now let's understand this whole and its parts from a real life example:
Example: In a class, there are 60% boys and 40% girls
Now, in this situation:
Class is a whole and boys & girls are its parts.
Also, values of parts i.e. boys and girls are 60% and 40% respectively.
Percentages can be :
Converted to Fractions
Converted to decimals
Explanation of these two topics(with examples) is available in the above links.
Study More Solved Questions / Examples
|
In a class there are 40 students. On Monday 4 students were absent. Find what percent of students were absent on Monday? |
|
Out of 18 glasses order by Jennny, 3 get broken while delivery. Find what percent got broken? |
|
In an election, total voting done was 1600. Candidate 'A' won the election and he got 1000 votes in total. Find the percentage of votes casted to the candidate 'A' ? |
|
Julie and Jenny order a pizza. Pizza was having 5 pieces out of which Julie ate 3 pieces and Jennny ate 2 pieces. Find what percent of pizza Julie and Jenny ate? |
|
In a town 35% are males, 25% are females. Find % of children ? |
|
In a class 20% students like painting. Total number of students in a class are 50. Find how many students like painting? |
|
In a city with population 5000, adults are 35%, olds are 25% and children are 40%. Find the population of males, females and children in this city ? |
|
In a class of 40 students, if girls are 40%. Find total number of boys ? |
| | |






