Before you study what is Parallelogram, you are advised to read:
What is a Quadrilateral ?
What are Parallel Lines ?
Definition of Parallelogram : A parallelogram is a quadrilateral in which opposite sides are equal and parallel to each other.
Example 1: In the following diagram of Quadrilateral ABCD
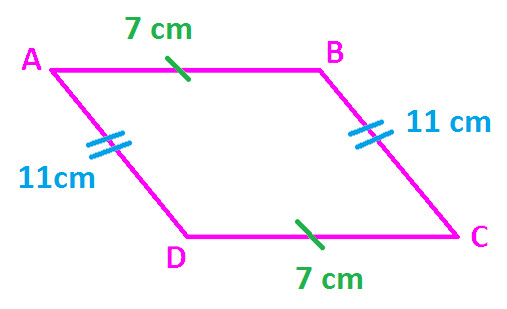
AB is parallel to DC
AD is parallel to BC
AB = DC = 7 cm
AD = BC = 11 cm
Hence, we can say Quadrilateral ABCD is a parallelogram.
Example 2: In the following diagram of Quadrilateral PQRS
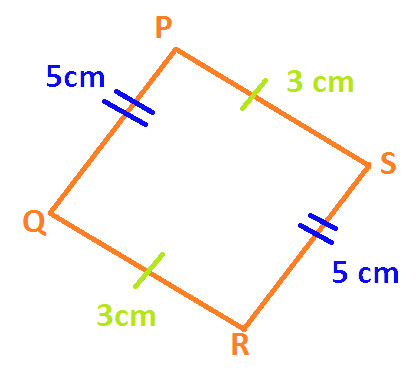
PQ is parallel to SR
PS is parallel to QR
PQ = SR = 5 cm
PS = QR = 3 cm
Hence, we can say Quadrilateral PQRS is a parallelogram.
|






