Before you understand the concept of exterior angles of polygon, you are advised to read:
Types of Polygon
Sum of measure of Exterior Angles of any Polygon is always equal to 360 degree
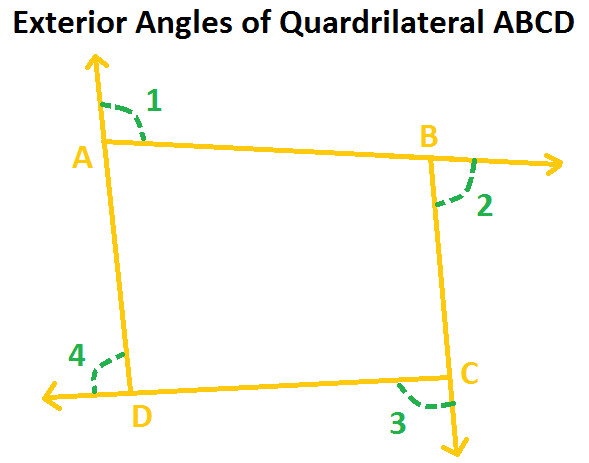
In the above diagram, Quadrilateral ABCD have angle 1, angle 2, angle 3 and angle 4 as their exterior angles.
So as per exterior angle property of a polygon, we get:
Angle 1 + Angle 2 + Angle 3 + Angle 4 = 360 degree
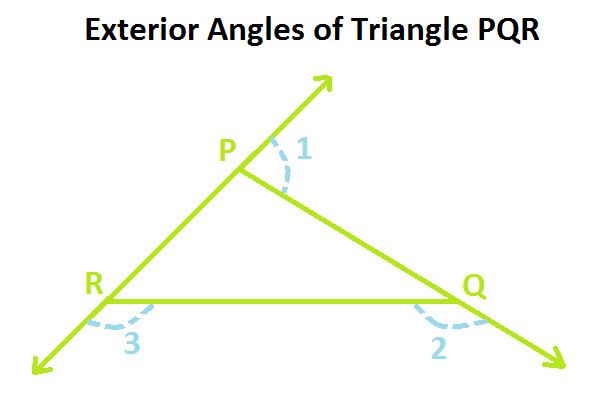
In the above diagram, Triangle PQR have angle 1, angle 2 and angle 3 as their exterior angles.
So as per exterior angle property of a polygon, we get:
Angle 1 + Angle 2 + Angle 3 = 360 degree
From above two diagrams, you can observe that what so ever is the type of polygon, the sum of measure of exterior angles of all types of polygon is always equal to 360 degree.
|






