Definition: A line segment which joins two vertices (other than adjacent vertices) is called Diagonal.
In other words, a line segment which joins opposite vertices, is referred to as "Diagonal"
In the following polygon:
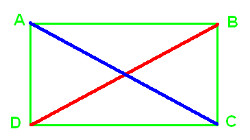
Line AC and DB joins opposite vertices i.e A & C and D & B respectively.
Hence AC and DB are the Diagonals of given Polygon ABCD.
Let study following figure also and find names of all Diagonals:
Figure 1:
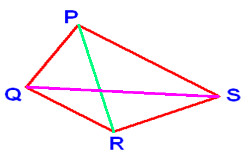
Line PR and QS joins opposite vertices i.e. P & R and Q & S respectively.
Hence PR and QS are the Diagonals of given Polygon ABCD.
Figure 2 :
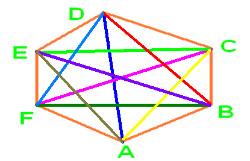
In the above figure, AE, AD, AC, BF, BE, BD, CE, CF & DF all are Diagonals.
|






