There are three properties of diagonals of parallelogram
Diagonals of Parallelogram are not equal.
Diagonals of Parallelogram bisect each other
Diagonals of Parallelogram are not equal
Example 1: Observe the following diagram of parallelogram:
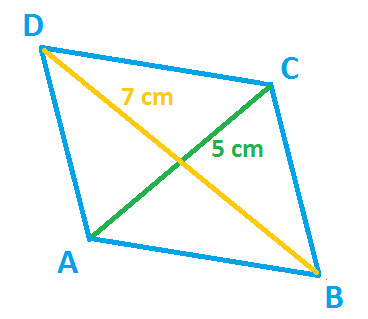
In the above diagram of parallelogram ABCD:
AC and DB are two diagonals
AC = 5cm
DB = 7 cm
This explains that diagonals of parallelogram are not equal
Diagonals of Parallelogram bisect each other
This property explains that diagonals of parallelogram bisect each other at the intersecting point.
In simple words, we can say that:
Diagonals of parallelogram divide into half at the point of intersection
Example 2: Observe the following parallelogram.

In the above diagram of Parallelogram ABCD:
AC and DB are two diagonals
AC = 5cm
DB = 7 cm
Both diagonals AC and DB intersect at point X
Since the diagonals of parallelogram bisect each other at the intersecting point, so we get:
AX = XC = 2.5 cm
DX = XB = 3.5 cm
|






