Before you understand Cartesian System, you are advised to read:
What is Number Line ?
Cartesian System was invented by French mathematician of 17th Century - Rene Descartes. He developed the idea of placing two perpendicular number lines over each another and locating points on these lines.
You can study Cartesian System in details with the help of following three diagrams:
Observe the following diagram 1 of Cartesian System:
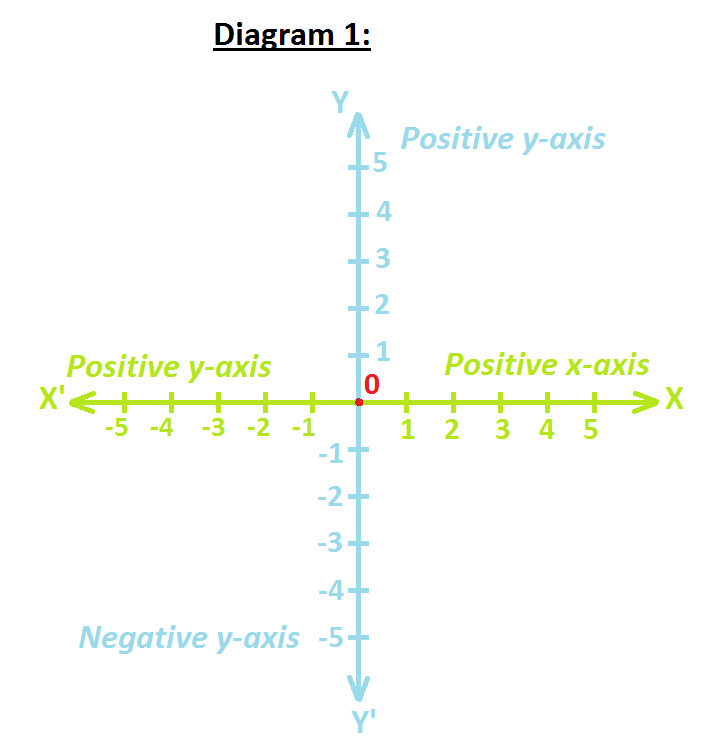
On observing you will notice the following points:
Among these two lines, one line will be horizontal and other will be vertical.
Mark Horizontal line is known as X'X and Vertical line as Y'Y.
Both line X'X and Y'Y intersects at a point and mark this point as 0.
The Horizontal Line X'X is known as x-axis.
The Vertical Line Y'Y is known as y-axis.
Since positive numbers lie on the OX & OY directions, so OX & OY directions are known to Positive x-axis and Positive y-axis respectively.
Since negative numbers lie on the OX' & OY' directions, so OX' & OY' directions are known as Negative x-axis and Negative y-axis respectively.
Now, observe the following diagram 2
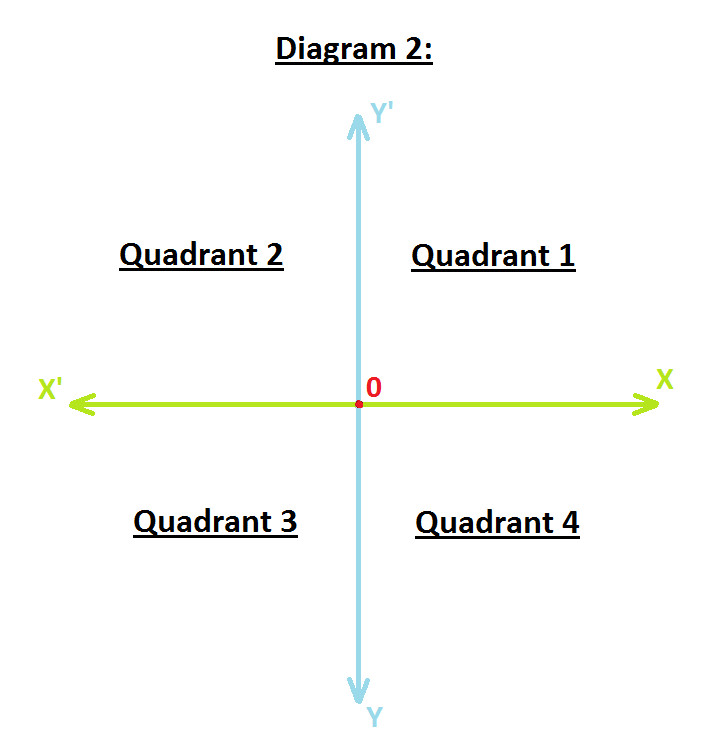
The diagram is divided into four quadrant i.e Quadrant 1, 2, 3 and 4.
The diagram is known as The Cartesian Plane or Coordinate Plane or The xy Plane.
The axes are known as Coordinate Axes.
Now, observe the following diagram 3:
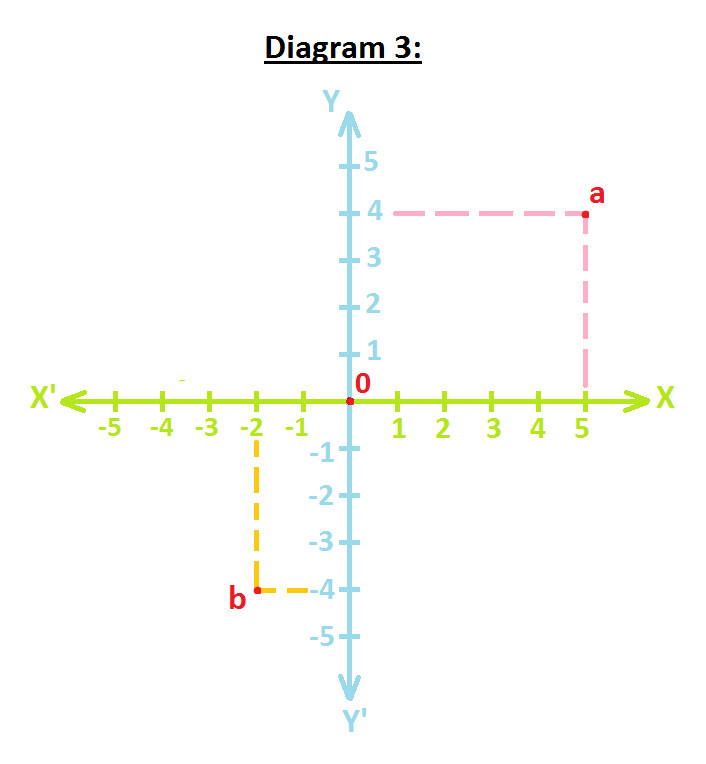
Let's understand how to write the coordinates of points a & b:
The x-coordinates of a point is equal to it's perpendicular distance from y-axis measured along the x-axis. The x-coordinates are; positive along the positive direction of x-axis and negative along the negative direction of x-axis.
So, for point 'a', perpendicular distance from y-axis along x-axis is 5. And since point 'a' lies on the positive directions (see diagram 1 to understand positive directions) its units is also positive i.e. 5
Similarly, for point 'b', perpendicular distance from y-axis along x-axis is (-2). And since point 'a' lies on the negative directions (see diagram 1 to understand negative directions) its units is also negative i.e. (-2)
The y-coordinates of a point is equal to it's perpendicular distance from x-axis measured along the y-axis. The x-coordinates are; positive along the positive direction of y-axis and negative along the negative direction of y-axis.
So, for point 'a', perpendicular distance from x-axis along y-axis is 4. And since point 'a' lies on the positive directions (see diagram 1 to understand positive directions) its units is also positive i.e. 4
Similarly, for point 'b', perpendicular distance from x-axis along y-axis is (-4). And since point 'a' lies on the negative directions (see diagram 1 to understand negative directions) its units is also negative i.e. (-4)
The x-coordinate is also known as abscissa.
The y-coordinate is also known as ordinate.
While stating the coordinates of point, x-coordinate is written first and then y-coordinate. So coordinates of point 'a' are (5, 4) and coordinates of point 'b' are (-2, -4).
|






