Before you study, how to find area of trapezium, you are advised to read:
What are Parallel Lines ?
How to find Area of Triangle ?
How to find area of Rectangle ?
Formula for calculating Area of Trapezium:
Area of Trapezium = Height ( Σ of || lines ) / 2
Also, note that area of trapezium is always in unit2 e.g. cm2 or m2 etc ...
Now, let's understand how formula for area of trapezium is obtained:
Observe the following diagram:
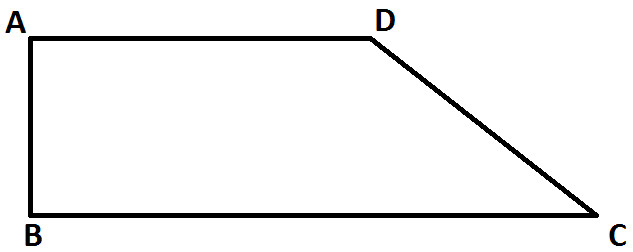
Above diagram represent Trapezium ABCD.
Let's draw a line segment DE parallel to side AB (as shown below)
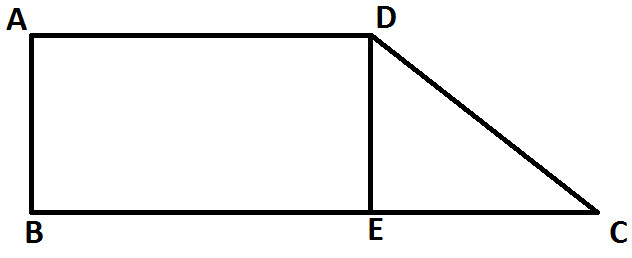
You can observe that here we got a rectangle ABCD and a triangle DEC
Now, recall formula for area of Rectangle and Area of Triangle & apply as shown below:
Area of Rectangle ABCD = Length X Breadth
Since length = AD and Breadth = DE, we get:
Area of Rectangle ABCD = AD X DE ..... (statement 1)
Area of Triangle DEC = 1/2 (Base X Height)
Since Base = EC and height = DE, we get:
Area of Triangle DEC = 1/2 (EC X DE)
Now, Area of Trapezium is equal to area of rectangle ABCD and area of triangle DEC; as shown below:
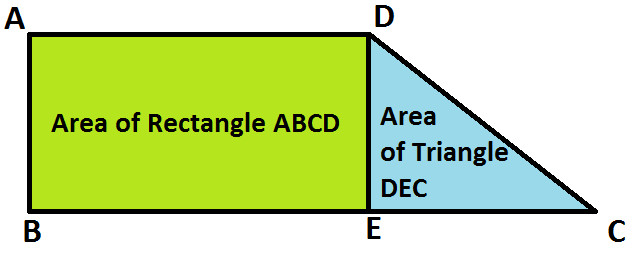
So we get:
Area of Trapezium ABCD = Area of Rectangle ABCD + Area of Triangle DEC
Put the values from above statement 1 & 2 and we get:
= [ AD X DE ] + [ 1/2 ( EC / DE ) ]
Take DE common and we get:
= DE [ AD + 1/2 EC ]
Balance the term in the bracket and we get:
= DE [ 2AD + EC ] / 2
Or we can write it as:
= DE [ AD + AD + EC ] / 2
Since AD = BE (opposite sides of rectangle are equal), so we get:
= DE [ AD + BE + EC ] / 2
See the diagram again, BE + EC = BC, so we get:
= DE [ AD + BC ] / 2
Now DE = Height , AD and BC are parallel lines, so we get required formula of trapezium:
Height ( Σ of || lines ) / 2
Let's use the formula to following example:
Example : Find the area of following Trapezium:
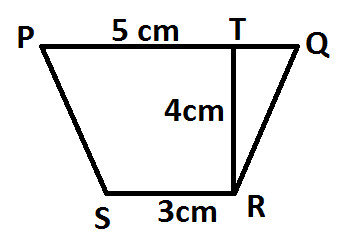
Solution: In the given diagram:
PQ and SR are parallel line of trapezium PQRS
PQ = 5 cm
SR = 3 cm
TR is the height of trapezium PQRS
TR = 4 cm
Apply the formula:
Area of Trapezium = Height ( Σ of || lines ) / 2
Or we can write its as:
= TR (PQ + SR) / 2
Put values of TR, PQ and SR from the above and we get:
= 4 ( 5 + 3 ) / 2
Solve brackets and we get:
= 4 (8) / 2
Solve division expression and we get:
= 4 (4)
Solve multiplication expression and we get:
= 16
Hence, area of trapezium PQRS is 16 cm2
|






