Angle of Elevation and find Height & Distance

Angle of Elevation

Angle of Depression

Before you study this topic you should know what is angle of elevation and depression: What is Angle of Elevation ? The formulas we used in angle of elevation : To find height and distance we use Tan θ = Opposite Side / Adjacent Side To find length or hypotenuse we use Sin θ = Opposite Side / Hypotenuse Example 1 : A person is standing 5m away from tree, the angle of elevation of the top of tree is 60° find the height of tree ? Solution : Let AB is the tree. B is the foot and A is the top of tree. 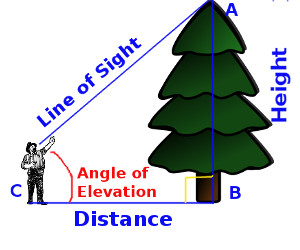C is the point on the ground where the person is standing and which is making the angle of elevation of 60° If we draw a picture it will look like as below - so we get CB (Distance from tree) = 5m ∠BCA = 60° Right angle is at point B AB (Height) = ? A right angle triangle △ ABC is formed in which AB is the Opposite Side from angle of elevation BC is the Adjacent Side from angle of elevation We know that Tan θ = Opposite Side / Adjacent Side tan 60° = AB BC √ 3  = AB 10 AB = 10 x √ 3  Value of √ 3  is 1.73 so, AB = 5 x 1.73 = 8.65 AB = 8.65m is the height of tree Example 2 :Height of tree is 8.65m, the angle of elevation of the top of tree is 60° find the distance at which the person is standing away from tree ? Solution : Let AB is the tree. B is the foot and A is the top of tree. C is the point on the ground where the person is standing and which is making the angle of elevation of 60° If we draw a picture it will look like as below - so we get CB (Distance from tree) = ? ∠BCA = 60° Right angle is at point B AB (Height) = 8.65m A right angle triangle △ ABC is formed in which AB is the Opposite Side from angle of elevation BC is the Adjacent Side from angle of elevation We know that Tan θ = Opposite Side / Adjacent Side tan 60° = AB BC √ 3  = AB 10 AB = 10 x √ 3  Value of √ 3  is 1.73 so, 8.65 = CB x 1.73 CB = 8.65 / 1.73 CB = 5 so the person is standing 5m away from the tree Example 3 : A tree is 5m high. If angle of elevation is 45° find the hypotenuse Let AB is the tree. B is the foot and A is the top of tree. C is the point on the ground where a person is standing and which the angle of elevation of 45° If we draw a picture it will look like as below - so we get AC = ? ∠ BCA = 45° AB = 5m A right angle triangle △ ABC is formed in which AB is the Opposite Side from angle of elevation AC is the Hypotenuse Side We know that Sin θ = Opposite Side / Hypotenuse sin 45° = AB AC    1    √ 2  = 5 AC AC = 5 x √ 2  Value of √ 2  is 1.41 so, 5 x 1.41 = 7.05 AC = 7.05m is the hypotenuse Study More Solved Questions / Examples At a point 20m away from the foot of a building, the angle of elevation of the top of building is 30° find the height of building At a point 10m away from the foot of a building, the angle of elevation of the top of building is 30° find the height of building At a point 10m away from the foot of a building, the angle of elevation of the top of building is 60° find the height of building A tower is 10m high. A steel wire is tied at the top of pole and is affixed at a point on the ground. If the steel wire makes an angle of 45° find the length of steel wire A mountain is 90m high. A steel wire is tied at the top of mountain and is affixed at a point on the ground. If the steel wire makes an angle of 45° find the length of steel wire A mountain is 50m high. A steel wire is tied at the top of mountain and is affixed at a point on the ground. If the steel wire makes an angle of 30° find the length of steel wire A pole is 30m high. A steel wire is tied at the top of pole and is affixed at a point on the ground. If the steel wire makes an angle of 30° find the length of steel wire A building is 70m high. A steel wire is tied at the top of pole and is affixed at a point on the ground. If the steel wire makes an angle of 30° find the length of steel wire